超詳細!超專業!Angry Birds極限完整版全解析!!
(轉載自Rhett Allain)
以下為全文編譯。
==================
當我正準備要完成綠色憤怒鳥的軌跡分析時,一件新鮮事吸引了我的注意。隨著Chrome版的憤怒鳥登場,我不得不分心先來看看究竟是怎麼回事。
Chrome版的憤怒鳥是在一般電腦上就可以玩,使我能用新的方法去補捉牠們的動態並進而分析。
先前無論是看youtube上其他人上傳的影片,亦或是自己用攝影機錄下我iPod上憤怒鳥的動作,我都著實費了一番工夫。
而現在,我可以用電腦螢幕擷取程式,輕鬆地在PC上抓取這些畫面。不過無論是用Quicktime's video capture或Snap Pro X,效果似乎都不太讓人滿意。前者的畫面幀數不夠高,後者也沒好到哪去。直到我發現一個免費的Java螢幕擷取軟體「screencast-o-matic.com」,效果顯然好得多。此外,用錄影機直接錄電腦畫面,也比錄iPod的畫面好多了。
不過我要用這些東西來幹嘛呢?當然是解答我一直以來的疑惑----
憤怒鳥的發射速度和角度有關嗎?
如果鳥確實是從「真實的」彈弓上發射,那麼理論上,水平射出的鳥速度應該要比垂直向上射出的鳥速度快。
為什麼?
請讓我用圖來解釋:

假設鳥的發射係數為一常數K,鳥的質量為m,在我知道發射的初始和結束位置,但不知道時間的前題下,利用「功能定理(Work-engergy Priciple)」就能求得我們要的數據。
假設「地球+鳥+彈弓」為一個系統,起始位置在y1=0,結束位置在y2=s。由於鳥一開始是處於靜止狀態,因此牠對於這個系統並沒有做功,如此一來,我們可以輕鬆地得到此系統的重力位能和彈性位能。透過功能定理我們可知:

或許這樣還不夠清楚,不過由於彈性位能=(1/2)ks^2,重力位能=mgy,所以上面的式子可簡化成:

但如果我們改改發射的角度呢?那會變成:

如此一來,初始的發射位置還是不變(y1=0),但結束位置需要改成:

再套用上面推導出的功能定理,可以得到終端速度為:
 因此我們可以得知,在發射角度等於0時,可以得到最大的發射速度(sin0=0)。
因此我們可以得知,在發射角度等於0時,可以得到最大的發射速度(sin0=0)。
P.S.當然,垂直往地面發射速度更大,但這麼做並沒有意義。
實例印證
我利用前面提過的螢幕擷取工具,可以得到這個圖表:
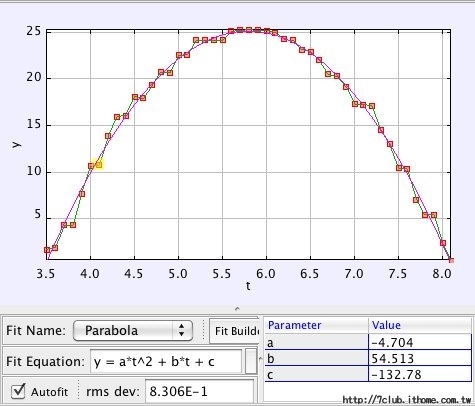
雖然加速度值看來正確(約-9.8m/s^2),不過由於錄製的影像並不連續,因此有些y值即便在不同時間(t),也出現了相同的數值。這並不讓人滿意,但沒辦法,只能用這樣的數據繼續推演。
接下來我要怎麼求得發射速度呢?首先是再藉由功能定理:

利用一次特定的實驗,我將鳥的初始發射位置定在4.355m,而最終鳥可以達到的高度是25.943m,我們可以求得鳥的y方向初速為20.58m/s。
至於x方向的圖表為:

從這條線的斜率我們可以求得x方向的速度是6.5m/s,換句話說,在這個角度下的發射速度是:

而這個角度是多少呢?透過速度的組成分析:
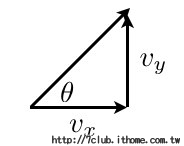
可以求得:

代入上面求得的x和y方向速度,得到發射角度為72.4度。至於透過錄影程式的追蹤功能,可以量出發射角度約為71.8度:

與公式推導幾乎相同。
接著,我再用相同的方式去追蹤(推算)其他的發射結果,並盡量讓錄製影片時沒有出現跳格的情況,以保證得到的數字夠精確。結果如圖:

於是我得到了8次發射的數據(4次錄影、4次螢幕擷取)。
假如憤怒鳥在製作時,的確有把發射角和速度的關係考慮進去,那理論上我把v^2和sinθ的關係圖描繪出來,應該要成一直線。而且事實上,如果我知道重力加速度(為一常數g)和彈弓後拉的長度(根據量測為2.2m),就可以畫出v^2和-2gs×sin(θ)的關係圖(斜率應為1),同時截矩為(ks^2)/m ,公式如下:

描繪結果:

好的,看起來結果的確是線性,不過斜率卻是5.34,而截矩為645。
這代表什麼意思?
重頭回去看看數據,發現幾乎所有測試的最終速度都在21.8m/s(靠下的7個點),只有一個遠遠偏離了這些數據。這一個偏離的測試,是在發射角度幾乎水平(仰角4度)的情況下產生的,而它的最終速度為26m/s。再清楚一點來說,由於發射角度接近水平,因此鳥在畫面中飛行的時間較短,這並不足以讓螢幕擷取程式得到夠多的數據。
如果我們單獨看這次測試的圖表:

就知道是因採樣數不足造成的誤差。
憤怒鳥用了虛擬彈弓
是的,這就是我的結論。在憤怒鳥裡的彈弓發射角度,並不會影響鳥的速度。更簡單一點講,不管你的發射角是幾度,鳥的發射速度都在22m/s左右,而這也可以合理解釋為什麼即使用了不同大小(重量)的鳥(例如黑色炸彈鳥或大隻紅鳥),牠們也都會在相同發射角的情況下,落在相同的位置。
憤怒鳥的世界,是一個全新的世界。
以下為全文編譯。
==================
當我正準備要完成綠色憤怒鳥的軌跡分析時,一件新鮮事吸引了我的注意。隨著Chrome版的憤怒鳥登場,我不得不分心先來看看究竟是怎麼回事。
Chrome版的憤怒鳥是在一般電腦上就可以玩,使我能用新的方法去補捉牠們的動態並進而分析。
先前無論是看youtube上其他人上傳的影片,亦或是自己用攝影機錄下我iPod上憤怒鳥的動作,我都著實費了一番工夫。
而現在,我可以用電腦螢幕擷取程式,輕鬆地在PC上抓取這些畫面。不過無論是用Quicktime's video capture或Snap Pro X,效果似乎都不太讓人滿意。前者的畫面幀數不夠高,後者也沒好到哪去。直到我發現一個免費的Java螢幕擷取軟體「screencast-o-matic.com」,效果顯然好得多。此外,用錄影機直接錄電腦畫面,也比錄iPod的畫面好多了。
不過我要用這些東西來幹嘛呢?當然是解答我一直以來的疑惑----
憤怒鳥的發射速度和角度有關嗎?
如果鳥確實是從「真實的」彈弓上發射,那麼理論上,水平射出的鳥速度應該要比垂直向上射出的鳥速度快。
為什麼?
請讓我用圖來解釋:

假設鳥的發射係數為一常數K,鳥的質量為m,在我知道發射的初始和結束位置,但不知道時間的前題下,利用「功能定理(Work-engergy Priciple)」就能求得我們要的數據。
假設「地球+鳥+彈弓」為一個系統,起始位置在y1=0,結束位置在y2=s。由於鳥一開始是處於靜止狀態,因此牠對於這個系統並沒有做功,如此一來,我們可以輕鬆地得到此系統的重力位能和彈性位能。透過功能定理我們可知:

或許這樣還不夠清楚,不過由於彈性位能=(1/2)ks^2,重力位能=mgy,所以上面的式子可簡化成:

但如果我們改改發射的角度呢?那會變成:

如此一來,初始的發射位置還是不變(y1=0),但結束位置需要改成:

再套用上面推導出的功能定理,可以得到終端速度為:

P.S.當然,垂直往地面發射速度更大,但這麼做並沒有意義。
實例印證
我利用前面提過的螢幕擷取工具,可以得到這個圖表:

雖然加速度值看來正確(約-9.8m/s^2),不過由於錄製的影像並不連續,因此有些y值即便在不同時間(t),也出現了相同的數值。這並不讓人滿意,但沒辦法,只能用這樣的數據繼續推演。
接下來我要怎麼求得發射速度呢?首先是再藉由功能定理:

利用一次特定的實驗,我將鳥的初始發射位置定在4.355m,而最終鳥可以達到的高度是25.943m,我們可以求得鳥的y方向初速為20.58m/s。
至於x方向的圖表為:

從這條線的斜率我們可以求得x方向的速度是6.5m/s,換句話說,在這個角度下的發射速度是:

而這個角度是多少呢?透過速度的組成分析:

可以求得:

代入上面求得的x和y方向速度,得到發射角度為72.4度。至於透過錄影程式的追蹤功能,可以量出發射角度約為71.8度:

與公式推導幾乎相同。
接著,我再用相同的方式去追蹤(推算)其他的發射結果,並盡量讓錄製影片時沒有出現跳格的情況,以保證得到的數字夠精確。結果如圖:

於是我得到了8次發射的數據(4次錄影、4次螢幕擷取)。
假如憤怒鳥在製作時,的確有把發射角和速度的關係考慮進去,那理論上我把v^2和sinθ的關係圖描繪出來,應該要成一直線。而且事實上,如果我知道重力加速度(為一常數g)和彈弓後拉的長度(根據量測為2.2m),就可以畫出v^2和-2gs×sin(θ)的關係圖(斜率應為1),同時截矩為(ks^2)/m ,公式如下:

描繪結果:

好的,看起來結果的確是線性,不過斜率卻是5.34,而截矩為645。
這代表什麼意思?
重頭回去看看數據,發現幾乎所有測試的最終速度都在21.8m/s(靠下的7個點),只有一個遠遠偏離了這些數據。這一個偏離的測試,是在發射角度幾乎水平(仰角4度)的情況下產生的,而它的最終速度為26m/s。再清楚一點來說,由於發射角度接近水平,因此鳥在畫面中飛行的時間較短,這並不足以讓螢幕擷取程式得到夠多的數據。
如果我們單獨看這次測試的圖表:

就知道是因採樣數不足造成的誤差。
憤怒鳥用了虛擬彈弓
是的,這就是我的結論。在憤怒鳥裡的彈弓發射角度,並不會影響鳥的速度。更簡單一點講,不管你的發射角是幾度,鳥的發射速度都在22m/s左右,而這也可以合理解釋為什麼即使用了不同大小(重量)的鳥(例如黑色炸彈鳥或大隻紅鳥),牠們也都會在相同發射角的情況下,落在相同的位置。
憤怒鳥的世界,是一個全新的世界。
